The Second Law in Classical vs. Chemical Thermodynamics
I have blogged quite a bit about how the concept of entropy and heat evolution have been erroneously equated. I'm not going to rehash that here, but rather set that aside and look at how the perspective of the Second Law of thermodynamics can lead to another misconception regarding the loss of energy.
Classical Thermodynamics
 Here is a formal definition of thermodynamics. It is the most literal and narrow one I could find. It applies pretty specifically to systems like a combustion engine, where heating a gas causes it to expand, and this expanding gas is contained in such a way as to do mechanical work by moving an object (in an engine this object is the piston). When fuel is combusted, an amount of heat is released equal to the difference between the chemical potential energy stored in the bonds of the reactants and the products. We can think of this "heat in" or "energy in" to the gas.
Here is a formal definition of thermodynamics. It is the most literal and narrow one I could find. It applies pretty specifically to systems like a combustion engine, where heating a gas causes it to expand, and this expanding gas is contained in such a way as to do mechanical work by moving an object (in an engine this object is the piston). When fuel is combusted, an amount of heat is released equal to the difference between the chemical potential energy stored in the bonds of the reactants and the products. We can think of this "heat in" or "energy in" to the gas. The second Second Law in this context, merely states that when converting this heat to mechanical work, you can never get 100% conversion. Thus Work Energy Out will always be less than Heat Energy In. But what happens to the rest? I've seen many folks describe this as energy that has essentially disappeared. No! As the simple depiction of a heat engine at right demonstrates, the heat that has not been converted to work is Heat Energy Out! Incorporating the symbols from the diagram, the First Law equation that applies is:
The second Second Law in this context, merely states that when converting this heat to mechanical work, you can never get 100% conversion. Thus Work Energy Out will always be less than Heat Energy In. But what happens to the rest? I've seen many folks describe this as energy that has essentially disappeared. No! As the simple depiction of a heat engine at right demonstrates, the heat that has not been converted to work is Heat Energy Out! Incorporating the symbols from the diagram, the First Law equation that applies is:
Heat Energy In = Work Energy Out + Heat Energy Out
or
Q1 = W + Q2
Note the width of the arrows in the diagram depicting conservation of total energy. In this context, then, the Second Law merely states that there will always be some Q2, which is another way of saying that:
W< Q1 always
The reason for this is that difficult-to-define concept of entropy. In mechanical contexts it appears that energy is disappearing. Since an engine is an open system, heat that is not converted to work does irreversibly dissipate into the surroundings. In reality, the thermal energy has not gone away, it will warm the surroundings, but this is often imperceptible (particularly if you are out of doors and not hovering nearby to the engine). Thus we associate entropy with dissipation and loss from the classical thermodynamics standpoint.
Chemical Thermodynamics
I trace my initial exposure to the concepts of thermodynamics to chemistry class in high school. Chemistry is the study of how matter interacts with other matter in the surroundings. First and foremost, in chemistry we are interested in:
- Can it react? -- Thermodynamics
- If so, how rapidly will it react? -- Kinetics
The Lazy Matter Principle
In chemistry, thermodynamics is often introduced in terms of what I like to call the Lazy Matter Principle. Chemistry is the study of how matter interacts with other matter, and the driving force of these interactions (reactions) is that all matter seeks out its lowest overall energy existence. This begins within the basic unit of matter -- the atom -- in how the electrons are oriented about the nucleus, how certain atoms may donate to, accept from, or share electrons with other atoms, and how the resulting molecule may be shaped or crystal arrangement is oriented. Electrical neutrality and charge distribution are major driving forces for this as well as governing interactions between molecules and within macromolecules such as large protein complexes.
Another driving force, particularly in gasses and liquids where molecules are free to move about, is the avoidance of collisions which would be a higher energy state. If you put a bunch of antisocial people in a room, you might find they'd distributed themselves relatively evenly about the room staking out their personal space and affording each the last amount of social contact. It is not unreasonable to think of this as the fundamental driving force for all matter, a drive towards this optimal state of disorder. Getting in the way of this, however, are the other factors previously discussed that would make for a more stable existence overall when matter is somehow associated with other matter.

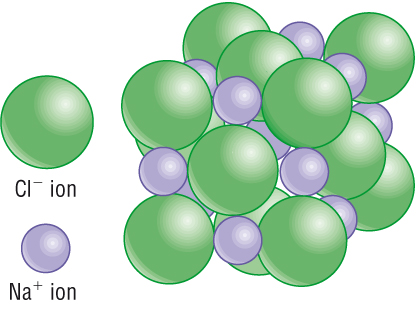
Take for example the chlorine atom, Cl. The electrons in this atom arrange such that the outer "shell" is missing a single electron. It "feels" incomplete, the complete shell is favored. The lazy antisocial Cl would prefer to be distributed evenly within whatever spacial constraints it is enclosed in. However, if there are sodium, Na, atoms around, they have a single electron in their outer shells. This electron is highly vulnerable to attack, and rather than defend a wider perimeter with one electron, Na readily gives up that electron for the stability of the filled shell (which is also a smaller space to defend). Thus Na becomes a positive ion, Na+ and a Cl will gladly take the electron and become the negative ion, Cl-.
They give up their individual electrical neutrality in exchange for the electronic preference. But if the oppositely charged ions pair off, then the compound we know as table salt, sodium chloride, NaCl, is formed. In actuality, there's no such thing as a single pairing of these two ions, but rather billions arrange in a crystalline pattern as shown here.
 What if there is no sodium around? Well then two chlorine atoms can share one of their electrons with the other so that each feels completed. This is Cl2, chlorine gas, which is the ground state (most stable form) of elemental chlorine. In both cases, we have different driving forces being balanced so as to minimize the overall energy state of the matter. We could think of this as matter trying to minimize its stress level much the way you might consider the overall positives and negatives of the major relationships in your life on your overall stress level and well being.
What if there is no sodium around? Well then two chlorine atoms can share one of their electrons with the other so that each feels completed. This is Cl2, chlorine gas, which is the ground state (most stable form) of elemental chlorine. In both cases, we have different driving forces being balanced so as to minimize the overall energy state of the matter. We could think of this as matter trying to minimize its stress level much the way you might consider the overall positives and negatives of the major relationships in your life on your overall stress level and well being.Heat of Reaction and Free Energy
So by now you might be wondering what the heck I'm doing going off on that tangent, but hopefully it makes sense in just a bit here. [Lots of what follows has been discussed elsewhere here on this blog, but I C&P sections to save you clicks]. In a chemistry class, you'll first learn about energy in reactions, also called the heat of reaction. For any reaction, we read left to right and call this the "forward reaction" and express the reaction as: Reactants → Products. Each component possesses some internal energy in the form of chemical bonds formed between atoms. This can be calculated from the basics by tallying up bond energies in all of the molecules, or by looking up the heats of formation for the various molecules involved on a table. Then:
ΔHrxn = Hproducts - Hreactants
The Δ notation reads "change in" and for any process is taken to be the final state minus the initial state.
 |
| image link |
If the reaction is exothermic (heat releasing), then the energy of the products is less than that of the reactants and ΔH is negative. Conversely, if the reaction is endothermic (heat absorbing), then the products contain more energy than the reactants and ΔH is positive. In order to distinguish the types of energy, the term enthalpy is often used when discussing H. An exothermic reaction would be enthalpically favored then, as the components of the reactants would seek their lower energy state oriented as the products.
This does not tell the full story, however. This is where the concept of entropy in chemistry context is introduced:
Entropy Definition: The measure of the disorder of a system, usually denoted by the letter S. A highly ordered system has low entropy
This is not a different entity from entropy in the classical application, but it makes more sense in the context of chemistry. An entropically favored reaction is one in which the reaction components become increasingly disordered.
Thermodynamics in chemistry is the prediction of what can happen, or what is energetically favored to occur. The Lazy Matter Principle restated: matter seeks its most relaxed state by balancing its drive toward low enthalpy/energy and high entropy/disorder. These two factors are related in a temperature-dependent fashion in what is called the Gibbs free energy, G. This is often called the "energy that is free to do work" as opposed to being somehow-or-otherwise made unavailable for this purpose. Gibbs free energy is related to enthalpy (energy) and entropy as follows:
ΔG = ΔH - TΔS
ΔFree Energy = ΔEnthalpy (Heat) - TempΔEntropy
Negative ΔG for a reaction as written is:
- Associated with the energetically favored direction of the reaction
- The direction in which the reaction will proceed spontaneously
- An exergonic reaction releasing energy that can be used to "do work"
- Assured when there is a negative change in enthalpy and a positive change in entropy
The thermodynamics do not tell us that the reaction will occur, or how rapidly a reaction will occur if/when it does, although they do offer some generalizations in this regard. A highly exergonic reaction (large -ΔG) is usually highly exothermic (large -ΔH), and such reactions generally proceed rapidly once initiated -- e.g. burning propane.
For the direction Reactants → Products
A: Spontaneous Reaction as Written: Regardless of magnitudes for enthalpy and entropy, both factors favor the products and these two "forces" combine to a negative ΔG. This reaction releases "free energy" to "do work" elsewhere. Note: As just stated, it would be erroneous to state that this reaction WILL occur, only that it CAN, and if it does, this is the direction it will proceed.
B: Reaction Won't Occur as Written: Below, the opposite situation is demonstrated. Here the enthalpy and entropy terms again combine in the same terms, this time favoring the reactants and a positive ΔG regardless of the magnitudes of ΔH and ΔS. Note: It is erroneous to interpret this as the reaction CANNOT occur. It won't occur spontaneously, but it can occur given energy input to the system, perhaps by being coupled to an exergonic reaction.
C: Enthalpy Favors Spontaneous Reaction , D: Entropy Favors Spontaneous Reaction. In these two scenarios below entropy and enthalpy "act" in opposite directions. The relative magnitudes of the ΔH and ΔS terms (and temperature) dictate which will dominate. When the dominant term favors the spontaneous reaction (results in a -ΔG), the reaction is said to be driven by that term.
This is the case for the left side depiction in C. The exothermic (-ΔH) term dominates, enthalpically driven, while entropy works against the reaction. If the endothermic term dominates, then ΔG is positive and the reaction is not spontaneous. On the far right in D, we have the opposite. The highly disordering reaction (+ΔS) dominates resulting in a -ΔG, the reaction is entropically driven and spontaneous. In this case, the enthalpy "requirement" represents energy "sequestered" by the reaction making less available to "do work" as free energy. If enthalpy dominates, ΔG is positive and the reaction is not spontaneous. Because it is multiplied by the temperature, T, the entropy term tends to be more relevant at high temperatures.
Classical vs. Chemical Thermodynamics
Classical vs. Chemical Thermodynamics
As I've mentioned several times, there are statements about entropy derived from the very specific context of a heat engine, that are not universally applicable to other contexts. No ... this does not mean that the Second Law changes or that those statements are inaccurate, just that context is everything. The context that is relevant to the human being is that of chemistry, not classical thermo. We are electrochemical systems, not thermodynamic in the classical sense.
Heat and Entropy:

C-Type Reaction: The Combustion of Methane
In a combustion engine, due to the Second Law, some amount of the heat energy is not available to do mechanical work. This is attributed to the the concept of entropy as dictated by the Second Law. A chemical reaction that is somewhat analogous to this would be the "C-type" combustion of methane.
CH4 + 2O2 → CO2 + 2H2O
ΔH = -890 kJ/mol , ΔS ≈ -5 J/mol·°KΔG at 298°K ≈ -888 kJ/mol
These values reflect only a small change in free energy due to the decrease in entropy, but there is at least an analogy here whereby some of the thermal energy released in the reaction is used to overcome the small unfavorable entropy change. And yet this conflicts with the idea that entropy increase is synonymous with thermal energy dissipation.
D-type Reaction: A Spontaneous Endothermic Reaction
In a general chemistry lab, energetics are usually introduced by observing exothermic and endothermic reactions. The student is often urged to feel the reaction vessel for a change in temperature: warming indicating heat evolution in an exothermic reaction, and cooling indicating an endothermic reaction that absorbs heat from the surroundings. Below is a video of one such endothermic chemical reaction that is spontaneous due to it's highly favorable increase in entropy (solid reactants to gas and liquid products).
Ba(OH)2.8H2O(s) + 2NH4Cl(s) → 2NH3(g) + 10H2O(l) + BaCl2(s)
ΔH = 164 kJ/mol , ΔS = 591 J/mol·°K
ΔG at 298°K = -12.1 kJ/mol
This seems counter intuitive, as products are at higher energy than the reactants and yet feel colder, but this is instructive to undo some of the misconception about heat and entropy that may have been borne from the context of classical thermo. If the heat produced in one chemical reaction is absorbed by another, we see that thermal energy has other uses and fates other than dissipation into the environment. At least some of the heat that is evolved "on paper" in our exergonic reactions (e.g. glucose and fatty acid oxidation) is "immediately" sequestered in the endergonic reactions (e.g. gluconeogenesis and de novo lipogenesis via ATP and/or reducing equivalentd). If there were reactions like the one above occurring in humans, we'd be having a harder time of it maintaining body temperature, and freezing tissues would be rather catastrophic. Luckily there aren't ... but this phenomenon still points to a use for heat generated besides that which will keep our bodies hovering around 37°C.
Lastly, it begins to become clear that entropy as synonymous with "reducing free energy available" is incorrect. Which brings us, finally, to ...
A-Type Reaction in Humans: Glucose Oxidation
Here are the thermodynamic values for the net oxidation of glucose to carbon dioxide and water:
C6H12O6 + 6O2 → 6CO2 + 6H2OΔH = -2801 kJ/mol , ΔS = +259 J/mol·°KΔG at 298°K = -2880 kJ/mol
This reaction is favored both from an enthalpy (energy) and entropy standpoint, and the "forces" combine. Note that the entropy here does NOT act in any way to make some amount of the heat produced in the exothermic reaction unavailable to do work. Rather, it contributes to the free energy available to do work.
Let that sink in for a moment.
Summary:
The above were presented to illustrate what the Second Law does and does not say about energy partitioning and the fate of thermal energy in the chemical reaction itself. Clearly, this is quite different from the narrow application to the heat engine involving thermal energy and mechanical work done by an expanding gas (PV work).
Irreversibility and Increasing Entropy:
Perhaps it's the specific way the Second Law is sometimes stated, or the term "irreversible" itself that adds the confusion. Consider (from MIT):
- The Second Law says that any process that would reduce the entropy of the isolated system is impossible.
- (In isolated system): If the change in state of the system is such that the entropy increases for the forward process, then for the backward process ... the entropy would decrease. The backward process is therefore impossible, and we therefore say that the forward process is irreversible.
There's an irony here! First, the "rub" against applying the First Law to humans is that "humans aren't closed systems". Well, this is true, but the Second Law as stated is referring to an ISOLATED SYSTEM. Thus if anything, as stated, it is the Second Law that does not apply to humans. Let me rephrase that lest someone say I'm claiming the Second Law doesn't actually apply to humans. Much in the same way that we need to account for energy transfer between open or closed (but not isolated) systems and the surroundings in First Law analyses, so too, the Second Law. However the statement of the Second Law specific to isolated systems is for all intents and purposes irrelevant to humans.
All chemical reactions are theoretically reversible. That is, if we introduce the huge caveat that they are NOT ISOLATED. They can be FORCED to go in reverse if a sufficient amount of energy is input into the system. It is impossible that they go in reverse "all by themselves" given the current conditions of the system (e.g. concentrations of types of matter and temperature), but it may be possible by changing these parameters and/or adding energy (thermal or otherwise) to the system to drive the reaction in reverse. Those reactions -- such as the combustion of methane and other hydrocarbons -- that we associate with irreversibility, simply are so overwhelmingly exergonic in one direction (usually as a result of being highly exothermic) as to be practically irreversible. It is, quite simply, "impossible" to harness the energy to drive them backwards
It should be readily apparent from the previous discussion that "irreversible spontaneous reactions" can involve an increase in the entropy of the system (C-type reactions). While this would seemingly violate the Second Law, it does not, and even some "mild" B-type (+ΔH, -ΔS) reactions can be run in reverse.
What if Everything You Were Ever Told About Entropy Turned Out To Be Wrong?
OK, I couldn't really think of a section title for this one, so I settled on the above. When you learn thermo in the classical sense, it is not wrong to associate entropy with a reduction in the energy available to do meaningful work. That's pretty much the definition of entropy in that context. What I've shown in this post is that in chemical thermo, this is not only not always the case. Indeed, when entropy drives a chemical reaction, it does so by INCREASING the free energy available to do work, not decreasing it. Furthermore, it often acts in convert with enthalpy in driving the reaction.
This is important only because of the misconception that somehow entropy is the thermodynamic back door through which some self-proclaimed metabolically advantaged people claim lose calories. But even this much isn't true.
I'm going to try to tie this in with human metabolism in a single follow up post. Wish me luck with that :-)
I'm going to try to tie this in with human metabolism in a single follow up post. Wish me luck with that :-)



Comments
Post a Comment
Comment Moderation is ON ... I will NOT be routinely reviewing or publishing comments at this time..